Haskell

The Illustrated Guide To Lazy Evaluation

Henry Dang General Programming, Haskell , ,

Most people would tell you that hard work and perseverance are important if you want to be successful, but sometimes it pays to be lazy.

When it comes to programming, however, being lazy has plenty of benefits, and lazy evaluation is just one of those examples. Lazy evaluation is the idea of delaying the evaluation of an expression until the very moment in which you need it.

Lazy evaluation is most commonly used in functional programming languages, and the one of highest notoriety is Haskell, which is a completely lazy language by default (unless you tell it not to be)

How’s Lazy Evaluation Work?

Imagine that you’re a UPS (United Postal Service) employee and your job is to deliver some packages to your customer’s doorsteps.

Unfortunately, you are notoriously also the worst employee in your department.

Unlike a good employee, you don’t respect “Fragile” labels. In fact, you’re not even aware that the package is fragile at all. That’s why in the interest of time, you hurl every package you have, directly onto the hard, unforgiving concrete of your customers’s yards.

Do your packages make it in one piece? Who knows! You never look inside the box. For all we know, the box could be a bunch of stuffed animals, or it could be a very expensive $2,000 laptop that’s as fragile as a piece of glass.

As far as you are concerned, you have a box, and you transport it to someone else. This “box” is the expression, and evaluating the expression would be like opening the box to see its contents. While there is also metadata about the box, like whether it’s fragile or not, you have no clue whether it’s fragile or not until you read the information off the box.

Simply put, the essence of lazy evaluation is that you don’t know what’s inside something until you look at it. Initially, this sounds pretty simple and obvious. If you don’t look inside the box, how can you know what’s in it?

And that’s where it takes a loop. All of these boxes act like the box in Schrödinger’s cat experiment.

When it comes to lazy evaluation, you have no clue what’s in the box, but also there isn’t actually anything tangible in the box either. In a lazy evaluation model, to get a result out of the box, you would need to open it, and the very act of opening it causes the value inside to come into existence. Prior to opening the box, the box is essentially empty (an unevaluated expression, to be precise). It weighs nothing, makes no noise, and otherwise acts exactly like a normal box.

This can give us some pretty neat results. For example, suppose you have an expression like 1 divided by 0. This is the expression, which in our analogy, is the box. In a language like Python or Java, you would immediately crash with a divide by zero error.

But in Haskell, you can have an expression like “div 1 0”, and as long as you don’t evaluate it, nothing happens! You don’t get an error, because until you evaluate “div 1 0”, it simply exists as an expression with no value. Once you evaluate it (open the box, in this case), Haskell finds that the value is erroneous, and an error pops out.

Going a step further, what if you had a list that contained all of the numbers from 0 to infinity? (denoted as [0, infinity])

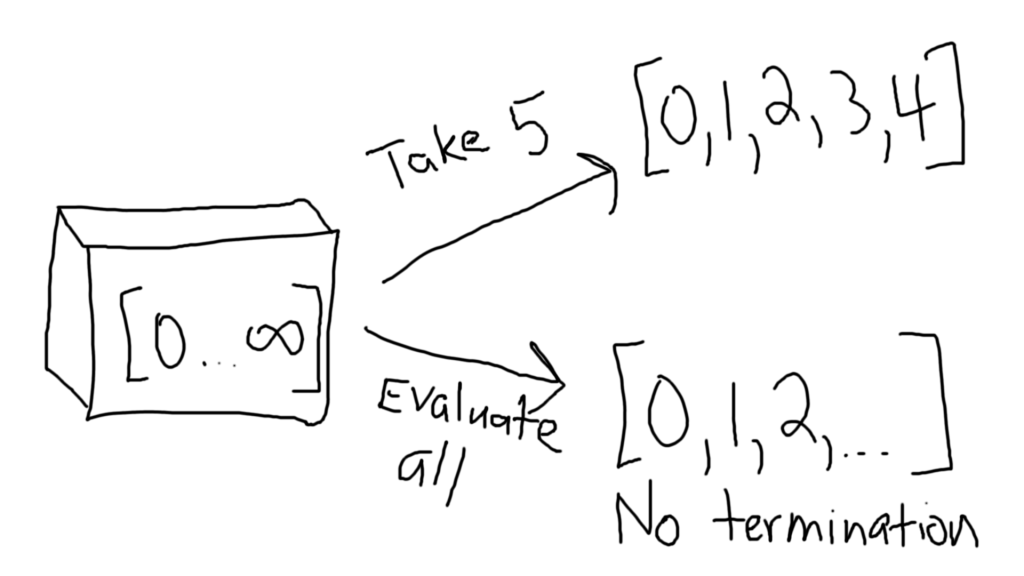
There is no doubt that this expression is infinite and contains all of the numbers from 0 to infinity. And yet, it doesn’t take up infinite memory, despite having an infinite size.

We can even take the first 5 terms out of this infinite list, and not crash. Why’s that? It’s because when you want to take the first 5 terms out, you evaluate only the first 5 terms in the list. As far as you are concerned, the other terms simply don’t exist, because you didn’t evaluate them into existence.

This means that you can pull finite results out of infinite lists, while also taking finite time and finite space. Note, however, that if you attempt to evaluate the entire list, it will end up taking infinite time, because each value of the list will materialize as each of the subexpressions get evaluated.

Consequently, if you tried to do anything like getting the length of the list, or trying to retrieve the last element in the list, you would not get a terminating result, because both of those require finding a final element, which doesn’t exist in the infinite list, and would require infinite evaluations to occur.

That sounds nifty and cool, but what about real-world applications?

If you’ve ever used a stream in any language (eg; Java streams), then you’ve used lazy evaluation. Streams, by nature, can be optimized by taking advantage of lazy evaluation.

In a real-world environment, streams can have millions to billions of elements. What if you wanted to concatenate two streams that each had at least 1 billion elements? Clearly, you can’t load either of the streams into memory, because that would quickly exceed memory limits.

This means you need to process the streams as abstract expressions, rather than as concrete values. Think of the streams as being two boxes, each containing potentially infinitely many items. With lazy evaluation, concatenating them together is a piece of cake — just put the two boxes inside of a new box.

At no point did you care about the insides of the stream, nor did you ever have to open the streams. This process has constant space and time complexity

With a non-lazy approach, you’d have to pull everything out of the second stream, find the ending element of the first stream, and then append each of the stream’s second elements one by one. Furthermore, you have to assume that no one adds any new elements into stream 1 as you’re appending the items in stream 2, which is a very big assumption to make. The reason the lazy approach doesn’t have this problem, is because you’re literally just stuffing the two streams into a new stream, without needing to know how many elements are in each of the streams, or what the elements are.

Conclusion

So with that, I hope you’ve gotten a better understanding of how lazy evaluation works. It has plenty of real-world use cases, and generally allows you to do operations on two, potentially infinite things, in constant time.

Lazy evaluation also allows you to defer errors until the very last moment, in which you have to evaluate an erroneous expression, at which point everything blows up. But if the erroneous expression is never needed (and thus never evaluated), then the error may as well not exist, which can be quite useful in some project workflows.

As a final note, lazy evaluation has some very notable drawbacks that you will need to be aware of. Firstly, if what you are doing is time-sensitive, like reading the current time, you will to immediately evaluate it on the spot.

This is because the “time” that you have is actually an expression that fetches the current time. The “current time” will actually be the time at which you evaluate it, and not the time at which the expression was created.

If you tried to time how long a program took to run by lazily fetching the start time, running the program, then lazily fetching the end time, you would find that both your start and end time are the same, and so it would output that the program took 0 seconds to run!

Hopefully, you’ve learned a bit about lazy evaluation from this article. There’s plenty more to learn about lazy evaluation, but the gist of it is that you can’t always use lazy evaluation.

As they old adage goes, sometimes, it pays to be lazy.

Everything in Haskell Is a Thunk

Henry Dang General Programming, Haskell , ,

There are a lot of misconceptions about Haskell.

Some people think everything in Haskell is a function. Others think that Haskell is just an implementation of Church’s lambda calculus. But both of these are false.

In reality, everything in Haskell is a thunk.

A thunk is a value that has not been evaluated yet. If everything in Haskell is a thunk, then that means that nothing in Haskell is evaluated unless it has to be evaluated.

From a non-functional programmer’s perspective, a thunk may initially seem to be a useless feature. To understand why thunks are useful, consider the following Python code.

x = 5 / 0

Traceback (most recent call last):
  File "", line 1, in 
ZeroDivisionError: division by zero

Unlike Haskell, Python evaluates the results immediately, which means that Python will crash as soon as an error occurs.

On the other hand, Haskell is different. In fact, you can string together dozens of lines of code, all of which contain an error, and no error will appear until one of those lines get evaluated.

let x = 3 `div` 0
let y = x

-- Can even divide x and y!
let z = x `div` y

let stringX = show x

-- Evaluate stringX, which
-- evaluates show x, which evaluates x
-- which finally evaluates 3 `div` 0, causing
-- the error to occur
putStrLn stringX

In this example, no matter what, Haskell will not give an error until something is evaluated. A common misconception is that a function call will always force the results to be evaluated, but that is simply not true.

In the example above, z is assigned the value of x divided by y, and yet there is no error. It is only when the value of stringX is evaluated via putStrLn (which prints a String) that Haskell throws an error.

One way to imagine thunks is to think of every value and function as being wrapped in a box. No one is allowed to peek into the box until the order is given. For all Haskell knows, the box could have anything in it, and Haskell wouldn’t care. As long as there are no type conflicts, Haskell will happily pass the box along.

In the code above, Haskell is fine with dividing two errors (both x and y, when evaluated, will give a division by zero error). However, it is only because x and y are both thunks, and Haskell doesn’t actually know the true values of x and y.

This gives Haskell the benefit of aggressively optimizing code, allowing for massive performance boosts.

Imagine if Haskell had an expensive function, F, that takes in one parameter, takes 10 seconds to run, and returns the evaluated value 5. Say that this same function also existed in Python.

If we were to run F ten times, we would find that Haskell only takes about 10 seconds to finish, while Python would take 100 seconds. Here, Haskell’s functional properties and lazy evaluation allows it to outperform Python.

In Python, functions are allowed to have side-effects. This means that if a Python function is run ten times, with the same input, it can give ten different results. On the other hand, for Haskell, if a function is run ten times, with the same input, it will always give the same result. This means that if there are multiple copies of the same function, called on the same input, Haskell can be certain that those results will all be the same. This is known as referential transparency, and it’s a feature that exists in most functional programming languages.

This property, combined with Haskell’s lazy evaluation, allows Haskell to memoize function calls. Now, if Haskell sees multiple copies of this expensive function called on the exact same input, it will simply evaluate one of the function calls, cache the result, and replace every future function call of F on that same input with the cached result.

What About Infinite Lists?

One consequence of everything being a thunk in Haskell is that Haskell is able to create infinite lists, and pass infinite lists around. In other words, Haskell is able to process and manipulate infinite lists as if they weren’t infinite, because they aren’t. Although the lists are technically infinite, Haskell only takes the elements that it wants.

For example,

let x = [1..]
let y = [1..]

x ++ y
-- concatenate all of x with all of y
-- to infinity
[1, 1, 2, 2, 3, 3, 4, 4, 5, 5 ...]

Here, x is stored to the infinite list from 1 to infinity, and y is stored to the exact same infinite list. Haskell is perfectly fine with storing these infinite data structures, because Haskell does not actually evaluate these structures until it needs to. When they are finally evaluated, they perform exactly like an infinite list — because that is exactly what x and y are.

In Haskell, treating everything as a thunk allows big performance boosts, and also gives the programmer the ability to store infinite data structures. So the next time someone says, “Everything in Haskell is X”, gently remind yourself that unless X is a thunk, they’re most likely wrong.