Haskell

The Illustrated Guide To Lazy Evaluation

Henry Dang General Programming, Haskell , ,

Most people would tell you that hard work and perseverance are important if you want to be successful, but sometimes it pays to be lazy.

When it comes to programming, however, being lazy has plenty of benefits, and lazy evaluation is just one of those examples. Lazy evaluation is the idea of delaying the evaluation of an expression until the very moment in which you need it.

Lazy evaluation is most commonly used in functional programming languages, and the one of highest notoriety is Haskell, which is a completely lazy language by default (unless you tell it not to be)

How’s Lazy Evaluation Work?

Imagine that you’re a UPS (United Postal Service) employee and your job is to deliver some packages to your customer’s doorsteps.

Unfortunately, you are notoriously also the worst employee in your department.

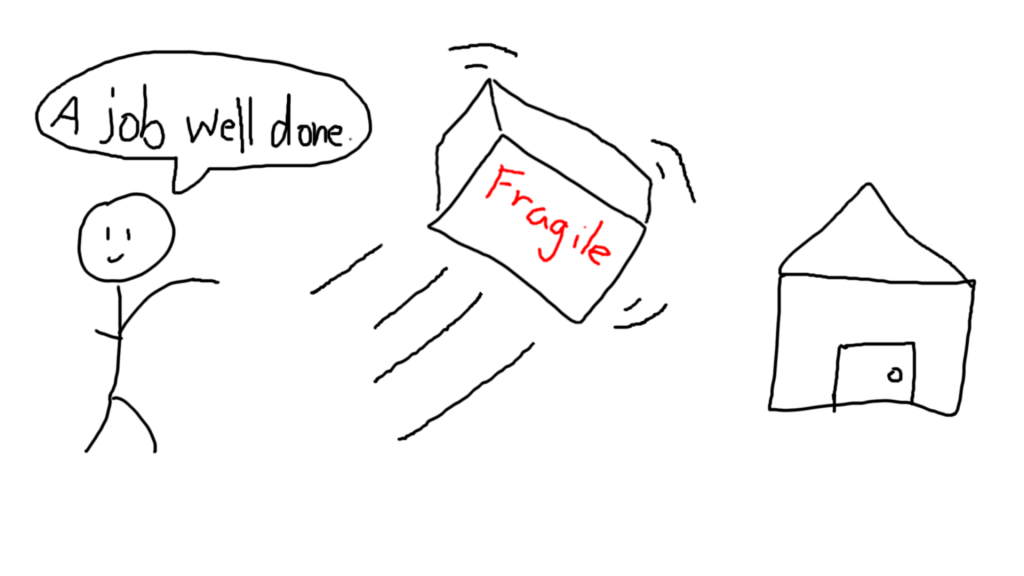
Unlike a good employee, you don’t respect “Fragile” labels. In fact, you’re not even aware that the package is fragile at all. That’s why in the interest of time, you hurl every package you have, directly onto the hard, unforgiving concrete of your customers’s yards.

Do your packages make it in one piece? Who knows! You never look inside the box. For all we know, the box could be a bunch of stuffed animals, or it could be a very expensive $2,000 laptop that’s as fragile as a piece of glass.

As far as you are concerned, you have a box, and you transport it to someone else. This “box” is the expression, and evaluating the expression would be like opening the box to see its contents. While there is also metadata about the box, like whether it’s fragile or not, you have no clue whether it’s fragile or not until you read the information off the box.

Simply put, the essence of lazy evaluation is that you don’t know what’s inside something until you look at it. Initially, this sounds pretty simple and obvious. If you don’t look inside the box, how can you know what’s in it?

And that’s where it takes a loop. All of these boxes act like the box in Schrödinger’s cat experiment.

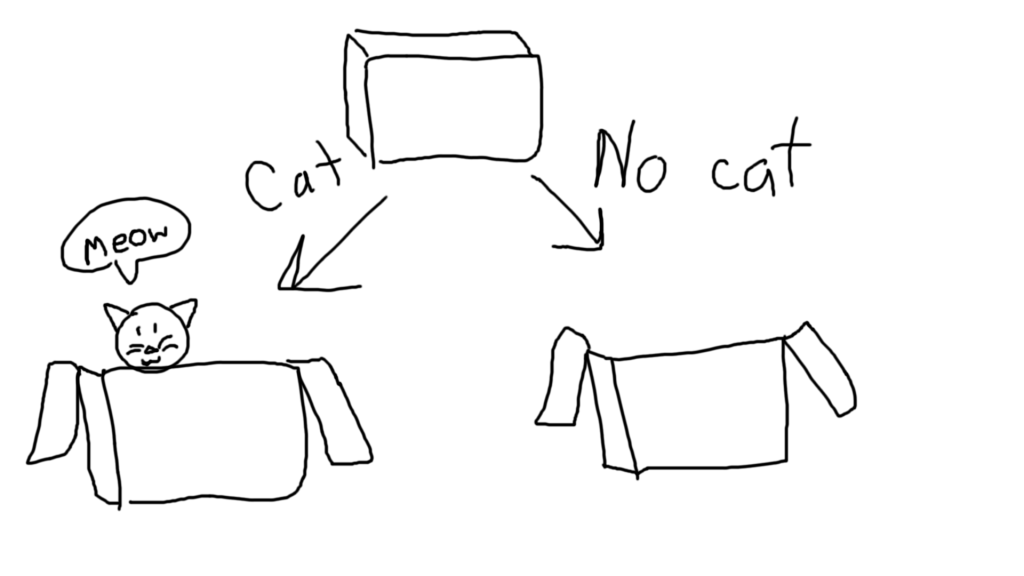
When it comes to lazy evaluation, you have no clue what’s in the box, but also there isn’t actually anything tangible in the box either. In a lazy evaluation model, to get a result out of the box, you would need to open it, and the very act of opening it causes the value inside to come into existence. Prior to opening the box, the box is essentially empty (an unevaluated expression, to be precise). It weighs nothing, makes no noise, and otherwise acts exactly like a normal box.

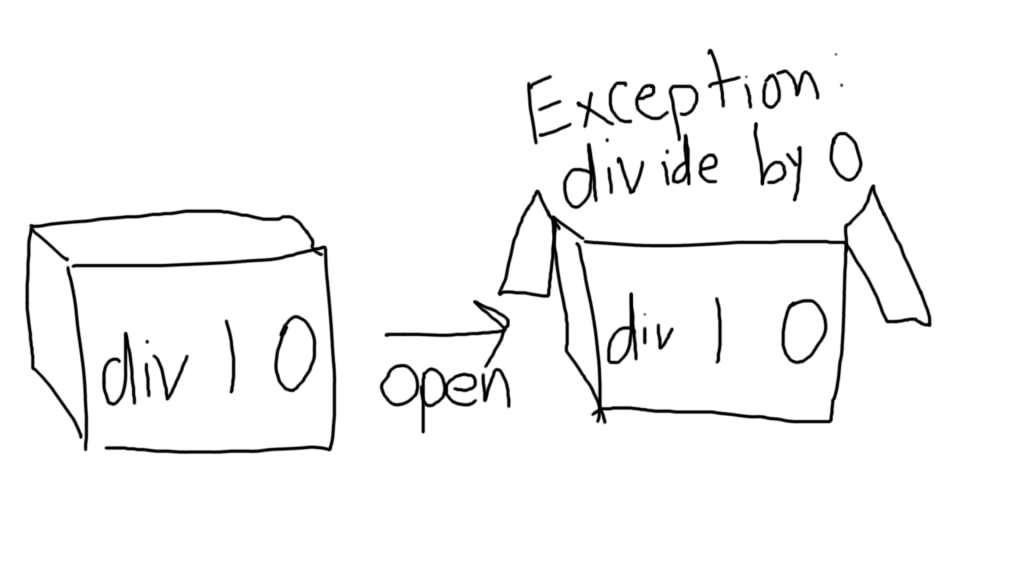
This can give us some pretty neat results. For example, suppose you have an expression like 1 divided by 0. This is the expression, which in our analogy, is the box. In a language like Python or Java, you would immediately crash with a divide by zero error.

But in Haskell, you can have an expression like “div 1 0”, and as long as you don’t evaluate it, nothing happens! You don’t get an error, because until you evaluate “div 1 0”, it simply exists as an expression with no value. Once you evaluate it (open the box, in this case), Haskell finds that the value is erroneous, and an error pops out.

Going a step further, what if you had a list that contained all of the numbers from 0 to infinity? (denoted as [0, infinity])

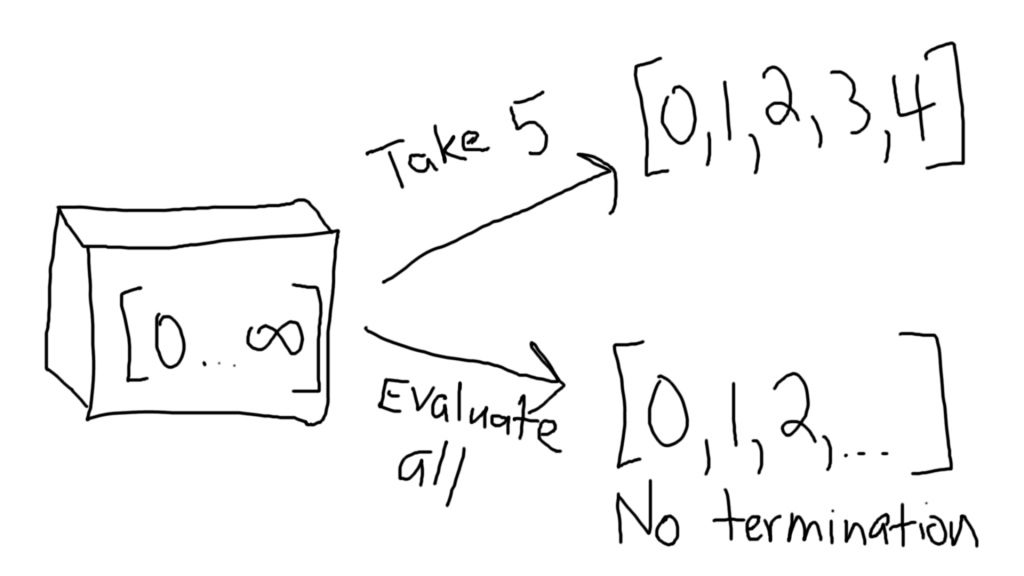
There is no doubt that this expression is infinite and contains all of the numbers from 0 to infinity. And yet, it doesn’t take up infinite memory, despite having an infinite size.

We can even take the first 5 terms out of this infinite list, and not crash. Why’s that? It’s because when you want to take the first 5 terms out, you evaluate only the first 5 terms in the list. As far as you are concerned, the other terms simply don’t exist, because you didn’t evaluate them into existence.

This means that you can pull finite results out of infinite lists, while also taking finite time and finite space. Note, however, that if you attempt to evaluate the entire list, it will end up taking infinite time, because each value of the list will materialize as each of the subexpressions get evaluated.

Consequently, if you tried to do anything like getting the length of the list, or trying to retrieve the last element in the list, you would not get a terminating result, because both of those require finding a final element, which doesn’t exist in the infinite list, and would require infinite evaluations to occur.

That sounds nifty and cool, but what about real-world applications?

If you’ve ever used a stream in any language (eg; Java streams), then you’ve used lazy evaluation. Streams, by nature, can be optimized by taking advantage of lazy evaluation.

In a real-world environment, streams can have millions to billions of elements. What if you wanted to concatenate two streams that each had at least 1 billion elements? Clearly, you can’t load either of the streams into memory, because that would quickly exceed memory limits.

This means you need to process the streams as abstract expressions, rather than as concrete values. Think of the streams as being two boxes, each containing potentially infinitely many items. With lazy evaluation, concatenating them together is a piece of cake — just put the two boxes inside of a new box.

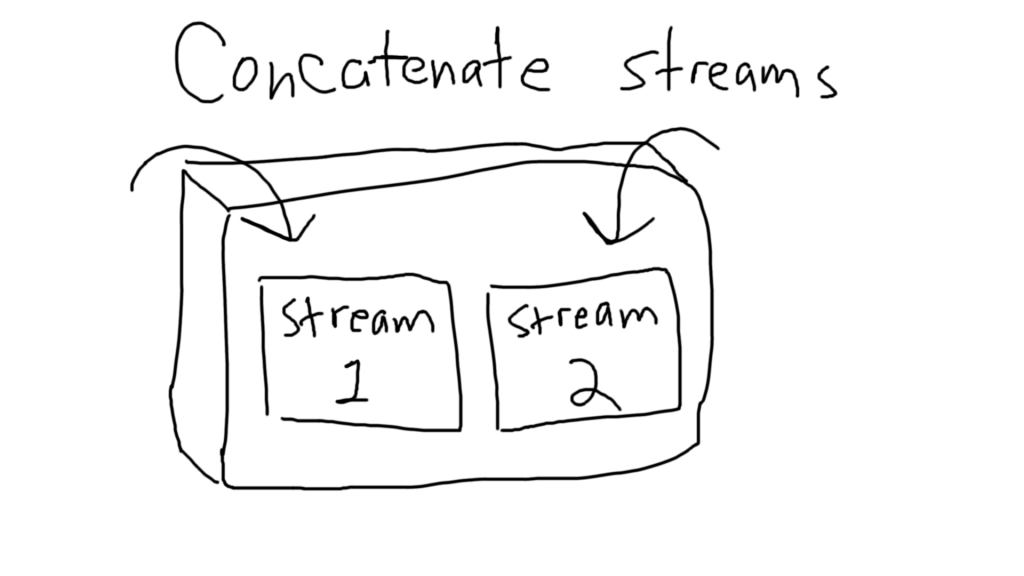
At no point did you care about the insides of the stream, nor did you ever have to open the streams. This process has constant space and time complexity

With a non-lazy approach, you’d have to pull everything out of the second stream, find the ending element of the first stream, and then append each of the stream’s second elements one by one. Furthermore, you have to assume that no one adds any new elements into stream 1 as you’re appending the items in stream 2, which is a very big assumption to make. The reason the lazy approach doesn’t have this problem, is because you’re literally just stuffing the two streams into a new stream, without needing to know how many elements are in each of the streams, or what the elements are.

Conclusion

So with that, I hope you’ve gotten a better understanding of how lazy evaluation works. It has plenty of real-world use cases, and generally allows you to do operations on two, potentially infinite things, in constant time.

Lazy evaluation also allows you to defer errors until the very last moment, in which you have to evaluate an erroneous expression, at which point everything blows up. But if the erroneous expression is never needed (and thus never evaluated), then the error may as well not exist, which can be quite useful in some project workflows.

As a final note, lazy evaluation has some very notable drawbacks that you will need to be aware of. Firstly, if what you are doing is time-sensitive, like reading the current time, you will to immediately evaluate it on the spot.

This is because the “time” that you have is actually an expression that fetches the current time. The “current time” will actually be the time at which you evaluate it, and not the time at which the expression was created.

If you tried to time how long a program took to run by lazily fetching the start time, running the program, then lazily fetching the end time, you would find that both your start and end time are the same, and so it would output that the program took 0 seconds to run!

Hopefully, you’ve learned a bit about lazy evaluation from this article. There’s plenty more to learn about lazy evaluation, but the gist of it is that you can’t always use lazy evaluation.

As they old adage goes, sometimes, it pays to be lazy.

Why You’ll Probably Never Use Haskell in Production

Henry Dang Haskell

If you’ve ever chatted with a Haskell programmer, you’ll probably hear that using Haskell in production is one of the greatest joys in life. But the grim reality is that Haskell just doesn’t quite work out in most corporate environments. As a pure functional programming language that was born from the depths of academia, there are several issues that make most developers hesitant to adopt Haskell.

So without further-a-do, I’m going to explain to you why you’ll probably never use Haskell in production.

 

Haskell isn’t a popular programming language

Unfortunately, the reality of Haskell is that very few people know how to code in Haskell, and even fewer are good enough to use it to the same level of productivity as the average Python or Java developer. This causes two big issues.

  1. Hiring a Haskell developer is much harder than hiring a Java, C++, or Python developer.
  2. Teams are unlikely to switch to Haskell because the majority of team members probably won’t know Haskell

Because of these two issues, it’s nearly impossible to use Haskell in production without having a team that is already fluent in Haskell. However, because it’s much harder to hire a Haskell developer than a Java/Python developer, it also becomes highly unlikely that a team of Haskellers will ever be formed.

One common argument is that if Haskell is a perfect fit for your business requirements, then you can just teach your team Haskell. After all, developers are capable of learning new technology stacks on the fly, so there’s no need for everyone to already know Haskell.

While this sounds good on paper, it’s not actually possible for developers to just “learn” Haskell, because…

 

Haskell has a massive learning curve

Any developer worth their salt should be able to learn a new OOP programming language in under two weeks. If you already know a couple of OOP languages, then learning another OOP language is incredibly easy, because all of your knowledge transfers over.

But Haskell doesn’t work in the same way, because it’s a completely different paradigm, and sets itself apart even from other FP languages. Its learning curve is by far the steepest out of any programming language I’ve worked with. Not to mention, it’s probably one of the few programming languages in the world where people will endorse reading and sharing research papers to learn Haskell.

That’s not all though, because when it comes to Haskell, your programming experience works against you. It doesn’t take two weeks to learn Haskell. It takes months to learn Haskell, and likely several more to be productive in it. The issue is that since you already have certain expectations of what programming is about, you’ll have preconceptions on how things might be done in Haskell. And all of those preconceptions will be wrong.

For example, in most OOP languages (eg; Java and C#), a function that returns an integer doesn’t really return an integer. It returns an integer or null, and this is a problem in Haskell. In Haskell, if your value has a chance of returning “null”, then you need to wrap it with the Maybe monad.

But why do we even need monads? In an OOP language, everyone got along just fine without them (mostly by doing null checks everywhere).  So why do we need monads in Haskell if we never had to use one in any other programming language?

And what is a monad anyway? Unfortunately, monads are notoriously hard to explain. They’re so hard, in fact, that there’s an entire meme about monad tutorials. Some people will tell you that monads are burritos, others will say monads are boxes, and really, none of them will do much to help you understand monads. You’ll have to work with monads in order to understand them, and when you do understand them, you’ll wonder why you were ever confused about them in the first place. 

When it comes to Haskell, monads are essentially brick walls for beginners. Most people will simply quit when they realize that almost every Haskell library in the world requires monads. But suppose someone does get over that gap. Understanding monads in general, and understanding monads in a standard Haskell library are two completely separate things, and so we see our third problem.

 

Haskell has very few mature and documented libraries

Technically, I’m cheating by listing two points in one, but they’re both very relevant to the issue at hand.

Firstly, when it comes to libraries, Haskell only has a handful of good libraries. These are the ones that almost everyone knows — Parsec, Yesod, pandoc, aeson, etc. These libraries have good documentation, in fact, some of them are spectacular, like how Yesod literally has a book for its documentation.

But those are just the mature and well-known libraries. But what if you want to use some relatively less well-known libraries? Tough luck, because those libraries almost never have any documentation.

In fact, when it comes to documentation, a lot of experienced Haskellers will tout that the only documentation they need are the function names and type signatures. And it’s true, you can usually figure out a lot from those two, and the Theorems for Free paper is a great read if you’re looking to learn more.

But is it really enough? For most developers, we want to see example code. For popular libraries, sure, there are thousands of examples, but for a smaller library? You’d be lucky for them to even have a useful README page. Working with poor, undocumented Haskell libraries is something you need to experience for yourself to understand why this is such a deal breaker.

All-in-all, Haskell’s poor library ecosystem makes it incredibly risky for anyone to use Haskell as a true “general purpose” programming language, because Haskell only has mature libraries for a small handful of fields. If your problem domain isn’t completely solved by some combination of Haskell’s popular libraries, then you should probably choose a different language.

 

Conclusion

If you’re looking to use a functional programming language in a production environment, Haskell is likely a bad call.

Very few people know Haskell to start with, and its insane learning curve means that it will take a long time before a developer reaches a proficient level with Haskell. Combine this with Haskell’s poor library ecosystem, and any plans for using Haskell in production will likely come to a grinding halt.

For a normal production environment, with a normal team, you are better off using F# or Clojure. Both of these languages have much more gentle learning curves, better documentation, and a huge library ecosystem since they were built with interoperability in mind. F# has complete access to all .NET libraries (and it’s directly supported by Microsoft!), and Clojure runs on the JVM, so you can run any Java library on it. Both of these are much safer choices than Haskell, and if neither of them work out, there’s always the option of using Scala (which also runs on the JVM).

But maybe you’re one of the lucky few who are working on a corporate Haskell project, and there are several examples, like how Facebook created Haxl and Sigma for spam detection.

But these are the exceptions, rather than the rule. Most of the time, people just want to get things done, and unless the stars align with you having exactly the right team with exactly the right problem, Haskell is almost never going to provide a solution that is the fastest, safest, nor the cheapest.

Everything in Haskell Is a Thunk

Henry Dang General Programming, Haskell , ,

There are a lot of misconceptions about Haskell.

Some people think everything in Haskell is a function. Others think that Haskell is just an implementation of Church’s lambda calculus. But both of these are false.

In reality, everything in Haskell is a thunk.

A thunk is a value that has not been evaluated yet. If everything in Haskell is a thunk, then that means that nothing in Haskell is evaluated unless it has to be evaluated.

From a non-functional programmer’s perspective, a thunk may initially seem to be a useless feature. To understand why thunks are useful, consider the following Python code.

x = 5 / 0

Traceback (most recent call last):
  File "", line 1, in 
ZeroDivisionError: division by zero

Unlike Haskell, Python evaluates the results immediately, which means that Python will crash as soon as an error occurs.

On the other hand, Haskell is different. In fact, you can string together dozens of lines of code, all of which contain an error, and no error will appear until one of those lines get evaluated.

let x = 3 `div` 0
let y = x

-- Can even divide x and y!
let z = x `div` y

let stringX = show x

-- Evaluate stringX, which
-- evaluates show x, which evaluates x
-- which finally evaluates 3 `div` 0, causing
-- the error to occur
putStrLn stringX

In this example, no matter what, Haskell will not give an error until something is evaluated. A common misconception is that a function call will always force the results to be evaluated, but that is simply not true.

In the example above, z is assigned the value of x divided by y, and yet there is no error. It is only when the value of stringX is evaluated via putStrLn (which prints a String) that Haskell throws an error.

One way to imagine thunks is to think of every value and function as being wrapped in a box. No one is allowed to peek into the box until the order is given. For all Haskell knows, the box could have anything in it, and Haskell wouldn’t care. As long as there are no type conflicts, Haskell will happily pass the box along.

In the code above, Haskell is fine with dividing two errors (both x and y, when evaluated, will give a division by zero error). However, it is only because x and y are both thunks, and Haskell doesn’t actually know the true values of x and y.

This gives Haskell the benefit of aggressively optimizing code, allowing for massive performance boosts.

Imagine if Haskell had an expensive function, F, that takes in one parameter, takes 10 seconds to run, and returns the evaluated value 5. Say that this same function also existed in Python.

If we were to run F ten times, we would find that Haskell only takes about 10 seconds to finish, while Python would take 100 seconds. Here, Haskell’s functional properties and lazy evaluation allows it to outperform Python.

In Python, functions are allowed to have side-effects. This means that if a Python function is run ten times, with the same input, it can give ten different results. On the other hand, for Haskell, if a function is run ten times, with the same input, it will always give the same result. This means that if there are multiple copies of the same function, called on the same input, Haskell can be certain that those results will all be the same. This is known as referential transparency, and it’s a feature that exists in most functional programming languages.

This property, combined with Haskell’s lazy evaluation, allows Haskell to memoize function calls. Now, if Haskell sees multiple copies of this expensive function called on the exact same input, it will simply evaluate one of the function calls, cache the result, and replace every future function call of F on that same input with the cached result.

What About Infinite Lists?

One consequence of everything being a thunk in Haskell is that Haskell is able to create infinite lists, and pass infinite lists around. In other words, Haskell is able to process and manipulate infinite lists as if they weren’t infinite, because they aren’t. Although the lists are technically infinite, Haskell only takes the elements that it wants.

For example,

let x = [1..]
let y = [1..]

x ++ y
-- concatenate all of x with all of y
-- to infinity
[1, 1, 2, 2, 3, 3, 4, 4, 5, 5 ...]

Here, x is stored to the infinite list from 1 to infinity, and y is stored to the exact same infinite list. Haskell is perfectly fine with storing these infinite data structures, because Haskell does not actually evaluate these structures until it needs to. When they are finally evaluated, they perform exactly like an infinite list — because that is exactly what x and y are.

In Haskell, treating everything as a thunk allows big performance boosts, and also gives the programmer the ability to store infinite data structures. So the next time someone says, “Everything in Haskell is X”, gently remind yourself that unless X is a thunk, they’re most likely wrong.