Year: 2020

The Illustrated Guide To Webhooks

Henry Dang General Programming, Software Development , , , ,

Imagine that you’re a software developer for a company that monitors nuclear reactors.

On average, every 1 hour, a warning gets triggered at any individual nuclear reactor. Since these warnings could lead to something catastrophic, they must be monitored in real-time, as every second counts.

Assuming you have one million clients, all of whom need to be notified, what’s an efficient way to do so, while also minimizing server load?

The Naive (And Terrible) Solution

The most straightforward way to solve this problem is to create an API that allows any client to ping your servers to figure out if any warnings have triggered.

At first glance, this looks like a good idea, since writing a RESTful endpoint like this isn’t particularly hard.

However, there’s a problem here. You know that on average, a warning only triggers every 1 hour.

You also know that the client is heavily concerned about these warnings, and since the client needs the warnings in “real-time”, let’s just conservatively assume that the client checks every 1 second for a warning.

Average number of warnings per hourNumber of times a client checked per hourAverage number of checks with no results (no warning found)
136003559
6036003540
120036002400
360036000

In the table above, you can see that there’s clearly a problem here. Regardless of the number of average warnings per hour, the client is still checking 3600 times an hour. In other words, as the average number of warnings goes down, the number of pointless checks goes up.

At 1 warning per hour, across 1 million clients, you would have over 3.5 billion unnecessary checks per hour. Even if we disregard how horribly inefficient this is, the real question is whether your servers can even comfortably handle that load without crashing.

Clearly, we can’t allow the client to grab the data on their own every 1 second, because this would cause a horrifically large amount of traffic (over 3.5 billion requests). Remember, at an average of 1 warning per hour, across 1 million clients, we should only have to send, on average, 1 million responses.

Sounds like a tough problem, but that’s where webhooks come in!

Introducing: Webhooks!

Webhooks are like reverse APIs. They’re like interviewers saying “Don’t call us, we’ll call you”.

Instead of having your clients ping your API every 1 second, you simply ping the client whenever a trigger occurs. Since you are only notifying the client whenever a warning occurs, it means that the client only gets notified when a warning exists. Therefore, there is no unnecessary traffic. You send out exactly 1 million responses, one per warning, and it’s still done in real-time.

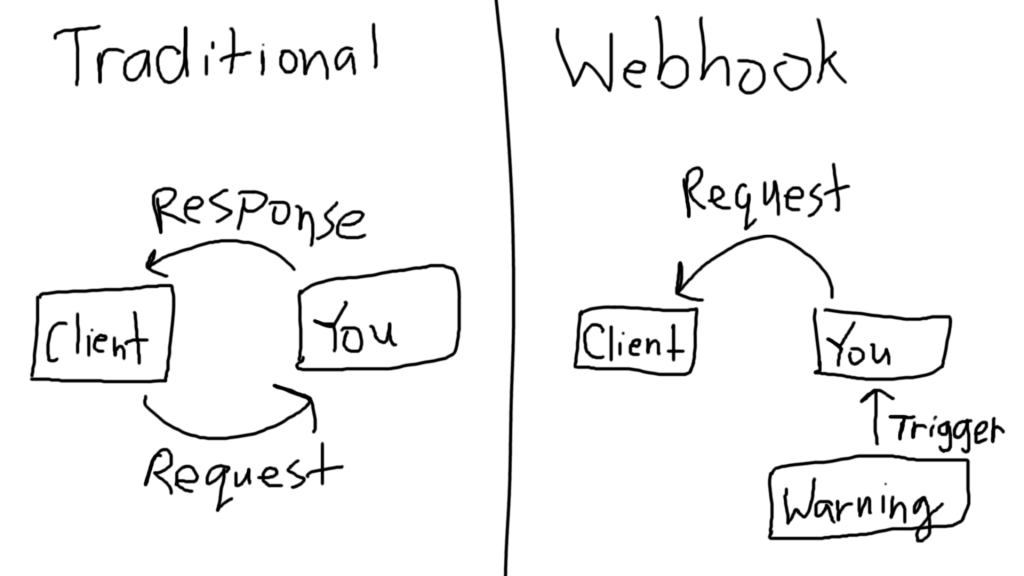
But how does the client “receive” the request?

Remember how I said a webhook is like a reverse API? The client is the one who writes the RESTful endpoint. All we have to do is record the URL to the endpoint, and each time the warning triggers, we send an HTTP request to the client (not expecting a response, of course).

What the client does with your POST’d request doesn’t matter. The client, in fact, can do anything they want, as long as their endpoint is registered with you.

This process can be generically applied to an infinite number of clients, by linking each client to the endpoint that they provided.

To summarize,

  1. Clients need to create a RESTful endpoint.
  2. Client gives you the URL to the endpoint.
  3. You save the endpoint somewhere.
  4. Anytime a warning triggers for that particular client, you send a POST request, with the warning enclosed, to the endpoint that they gave you.
  5. Client receives the POST request automatically, in real-time, and handles the warning in whatever fashion they want.

Conclusion

A webhook is an incredibly useful and simple tool that allows you to send data to clients in real-time based on some event trigger. Since the data is sent immediately after the event trigger, webhooks are one of many effective solutions for real-time event notification.

Additionally, since webhooks work in a “don’t call us, we’ll call you” fashion, you will never have to send a request unless an event trigger happens, which results in much lower server traffic.

In the example given above, at 1 warning per hour, across 1 million clients, using webhooks reduces the number of API calls from over 3.5 billion per hour to exactly 1 million per hour.

So the next time you have a situation where you need to notify clients based on some sort of event trigger, just remember this simple motto — “Don’t call us, we’ll call you”.

The Illustrated Guide to Semaphores

Henry Dang General Programming, Software Development , , ,

You are the receptionist at a very fancy Michelin-star restaurant. Due to COVID-19 restrictions, you can only allow 10 people in at a time, and if there are ever more than 10 people in the restaurant at the same time, the restaurant loses its license and shuts down.

How do you enforce this? One way you can do it is by using semaphores. To the receptionist, a semaphore is like a counter.

Initially, the semaphore starts at 10, representing that there are 10 empty spots in the restaurant. When someone enters the restaurant, they are “acquiring” the semaphore. Each time someone acquires the semaphore, they get to enter the restaurant, and the semaphore decrements by one.

As soon as the semaphore hits 0, that means that the restaurant is full, and so we can’t allow any more people in. At this point, anyone who tries to enter the restaurant by acquiring the semaphore will block. Remember that each person can act independently (ie; they’re separate threads), so this means that as long as the semaphore is 0, everyone who tries to acquire it, even if they cut in line, will inevitably have to wait.

So what happens when someone leaves the restaurant when the semaphore is at 0? When someone leaves, they “release” the semaphore. Ordinarily, this will increase the semaphore by 1, but if someone is blocked on the semaphore, like the two customers above, one of the two customers will get unblocked by the release, allowing one (and only one) of them to get in. When this happens, the semaphore remains at 0 since there are still only 10 people in the restaurant (one left, one entered, so there is no change).

Now here comes the interesting part. There are two types of semaphores. The first type is a “fair” semaphore. A fair semaphore acts like a normal line. If the semaphore is 0, the first person who finishes the acquire call and gets blocked, is also the first person to get unblocked when a customer leaves and releases the semaphore. Thus, it acts like a standard queue.

A tiny caveat is that it’s the first person who finishes the acquire call, not the first person who makes the acquire call. If Bob calls acquire first, then John, but John’s acquire call resolves before Bob’s, then John will be the first to get unblocked.

The other type of semaphore is an unfair semaphore. An unfair semaphore is different in that it doesn’t guarantee that the first person who blocks is also the first person to unblock. With an unfair semaphore, as soon as one person (thread) exits, it’s like a mad crowd of people all trying to get in at once, with no sense of order or fairness in sight.

Because of this, it’s not exactly a good idea to use unfair semaphores if you’re waiting in line at a restaurant. Suppose there was a man in line, and he failed to get into the restaurant after someone left. What would happen if he was super unlucky, and failed to get in even after a really long time?

This situation is called starvation, and it occurs when a thread (person) is continuously unable to do some sort of work due to being blocked or forced to wait. In this case, a customer is unluckily unable to enter the restaurant, because they never get chosen to get unblocked by the semaphore.

In the example image above, the semaphore counter is currently 0. Bob is the one wearing the blue hat, and he is blocked.

A new person arrives in step one and blocks on the semaphore. Then in step 2, someone leaves, and releases the semaphore. In step 3, the newly arrived person gets unblocked by the semaphore, allowing them to enter.

This leaves poor Bob in step 4 to starve. Then, it loops back to step 1, and the whole process repeats over and over again, guaranteeing that Bob never gets into the restaurant. In this scenario, Bob starves, both literally and in the programming sense.

Now, this is a very particular scenario, and it’s highly unlikely that Bob will continuously get blocked over and over again for an infinite amount of time. Depending on how unlucky Bob is, and how many people Bob is competing with, Bob could be stuck waiting for months or even years.

Conclusion

So based off these results, you’re probably thinking something like, “Oh, that sounds awful. Guess I’ll just use fair semaphores instead of unfair semaphores.”

Unfortunately, it’s not always best to choose fair semaphores. If fair semaphores were faster than unfair semaphores, and had better utility, then no one would ever use unfair semaphores.

When using a fair semaphore, you have additional overhead because you need to remember the exact ordering of who called acquire first, which makes them slower than unfair semaphores who will just randomly pick the first free thread that it sees.

The main reason to use a semaphore is when your problem has a limited resource, typically some sort of resource pool, that needs to be shared with other threads. You want the semaphore to be the size of the number of resources so that it blocks when all of the resources are gone, and unblocks when some thread releases their piece of the resource pool.

Lastly, remember that a binary semaphore (a semaphore whose value initializes at 1) is not the same as a mutex lock, and you generally shouldn’t use a binary semaphore in place of a mutex. Mutex locks can only be unlocked by the thread that locked it, whereas semaphores can be released by any thread, since it has no sense of ownership.

For most intents and purposes, a binary semaphore can basically act as a lock. However, you really shouldn’t say that a mutex lock is just a binary semaphore, because saying that is like saying that a car is an umbrella. It’s technically true, since a car covers you from the rain, but any normal person would look at you as if you had two heads.

How To Become An Elite Performer By Using Multi-Tenant Architecture

Henry Dang DevOps, General Programming, security, Software Development , , , , , , , , ,

Multi-tenant architecture, also known as multi-tenancy, is the idea of having your users (also known as tenants) share a pool of resources on a single piece of hardware.

To understand multi-tenancy, imagine you had a single computer, running a single program. Multi-tenancy is like having multiple applications run on one computer, while single-tenancy is like buying a new computer each time you had to open a new application.

Let’s suppose opening a YouTube video on Google Chrome counted as one program (and that you couldn’t open a new tab on Google Chrome). This would be the result:

However, unlike new Google Chrome instances, every tenant’s data is logically separated, such that no tenant has access to another tenant’s data, unless they have permission to do so.

The two main reasons to use single-tenancy architectures is

  1. They’re really really easy to setup. For the most part, you usually just have to give each tenant their own private database. Also, if your tenant needs a specific kind of environment that no other tenant uses, this is also easy to do, because each tenant can have their own private environment. Suppose one tenant wants to use PostgreSQL, another one wants to use MySQL, and third wants to use OracleDB. Assuming you have an interface to handle different types of databases, that would be no problem at all, because each tenant has their own database.
  2. It’s “more secure” than multi-tenancy architectures. Proponents of single-tenancy architectures will say that since you’re sharing resources on a single piece of hardware, you might have huge security vulnerabilities. This is because your tenants are typically separated by virtual machines/containers, with these VMs/containers being on the same computer. It stands to reason then, that if someone finds a vulnerability in the hypervisor that you’re using, then they can escape the VM/container (also known as a hypervisor attack) and theoretically access every tenant’s data on that machine.

Note that point 2, while a potential concern, is not really much of a concern. There are very few organizations that care more about security than the NSA (National Security Agency), and even the NSA reports these kinds of shared-tenancy vulnerabilities are incredibly rare, and that there “have been no reported isolation compromises in any major cloud platform”. Should you be afraid of hypervisor attacks over the massive cost savings of a multi-tenancy architecture? Probably not.

Now that you understand the basics of multi-tenancy architectures, let’s talk about why elite performers use multi-tenancy architectures.

Elite Performers Are Lightning Fast

The five essential characteristics of cloud computing, according to Accelerate’s State of DevOps 2019 Report, are:

  1. On-demand self-service (allow the consumer to provision resources)
  2. Broad network access (works on most platforms)
  3. Resource pooling (multi-tenancy)
  4. Rapid elasticity (rapid scaling)
  5. Measured service (can control optimize, and report usages)

Of these five characteristics, resource pooling, rapid elasticity, and measured services are all directly related to, or made easier with multi-tenancy. In other words, just by using a multi-tenancy architecture, you should already have three of these five things checked off, assuming you are following generally good practices. On-demand self-service and broad network access can be equally easily done with either single-tenancy or multi-tenancy architectures.

It should come to no surprise, then, that “elite performers were 24 times more likely to have met all essential cloud characteristics than low performers”. So clearly, the elite performers are using multi-tenancy architectures, but what’s the material gain?

Image courtesy of Accelerate’s State of DevOps 2019

More deployments, faster deployments, faster recoveries, and fewer failures. And not just by small margins either, recovering from incidents 2604 times faster is like the difference between recovering from an issue in a week, and recovering in just under 4 minutes.

Elite Performers Are Worth Their Weight in Gold

So how much exactly are elite performers saving with multi-tenancy architectures? According to Accenture, their work with police departments in the UK to switch over to multi-tenancy architectures will save a projected estimate of $169 million pounds (~$220 million USD). And on top of that, by making this switch, they claim that “time and workload gains in incident reporting can be upwards of 60%”. While switching to a multi-tenancy architecture is not easy, those are huge savings, brought mostly in part due to centralized data.

In multi-tenancy architectures, every tenant shares the same database, which makes sharing data much easier. According to Accenture, the average state in the U.S. has “300 different record systems”. That means that in the U.S.’s law enforcement agencies, there should be a minimum of 15,000 different databases.

Imagine you had to fetch data from 15,000 different databases. You don’t have access to any of them, and they’re all potentially in different formats with no national standardization. How do you coordinate such a massive task? Sure, you could email every single enforcement agency and have them manually share their data with you, but that would take on the scale of months to years.

Now imagine that all law enforcement agencies shared one database, with a handful of different standardized schemas. If you wanted to access a list of known offenders in Texas and Ohio, and merge them with some other table, you can do so without having to first convert everything into a standardized format, because they’re guaranteed to be in the same format. This makes everything incredibly easy to handle, and best of all, you can access them on-demand because the data is centralized, so you can get them instantly if you have admin-level authorization.

Elite performers who use multi-tenancy architectures save money, and accelerate data sharing. With savings like these, elite performers are absolutely worth their weight in gold.

Conclusion

Elite performers use multi-tenancy architectures, and while it’s true that using a multi-tenancy architecture won’t automatically turn you into an elite performer overnight, it will certainly set you on the right path.

Following good cloud computing practices is essential to speeding up development times and reducing costs. If you are interested in learning more, I strongly advise you to read Accelerate’s State of DevOps 2019, which is sponsored by Google, Deloitte, Pivotal, and other great tech companies.

One of the best ways to improve at your craft is to just copy the best. Is it original and creative? Not at all. But is it effective? Absolutely.

The Theater Student’s Guide To Passing Coding Interviews

Henry Dang General Programming, shakespeare ,

You’re not quite sure how you ended up in this situation.

You, a theater major and Shakespeare enthusiast, are currently stuck in a whiteboard programming interview.

What’s the catch? You have no programming experience, and you’ve never attended a programming class in your life.

The interviewer rattles off his first question.

“Let’s start with Fizzbuzz. Write a program that prints the numbers from 1 to 100. If it’s a multiple of 3, print ‘Fizz’. If it’s a multiple of 5, print ‘Buzz’. If it’s a multiple of both 3 and 5, print ‘FizzBuzz'”.

You furiously furrow your brows, frantically thinking of a way to pass this coding test. You look at the position’s job description, but you don’t recognize any of the programming languages in the description.

“What programming languages am I allowed to use?”, you ask.

“Oh, feel free to use any language you want.”

Suddenly, your eyes light up.

“Any language you say?”

Like any good theater student, you are well-versed in Shakespearean language, and so you confidently walk up to the whiteboard to begin drafting your solution.

“I’ll be using the Shakespeare Programming Language. First, we’ll need a dramatic title for our play. Let’s call it ‘The Elucidation of Foul Multiples'”.

And like a play, no program is complete without its supporting actors. Let’s add in our cast of actors from Romeo and Juliet, with an added bonus of Prince Henry, because why not.


The Elucidation of Foul Multiples.

Romeo, the hopeless romantic.
Mercutio, the grave man.
Prince Henry, the noble.
Ophelia, the drowned.

And just like how a computer program has code and functions, a play has acts and scenes.

Let’s introduce our first scene and act, so we can start cracking at this Fizzbuzz problem.


                    Act I: The Revelation Of Wretched Multiples.

                    Scene I: Romeo The Sweet Talker.

[Enter Prince Henry and Romeo]

Romeo: 
  You are as rich as the sum of a handsome happy honest horse and a lovely fellow. 
  Thou art the square of thyself.

[Exit Prince Henry]

[Enter Ophelia]

Romeo: 
  You are the sum of a beautiful blossoming daughter and the moon.
[Exit Ophelia]

[Enter Mercutio]

Romeo: 
  You plum.

To start off our beautiful play, we need to setup the drama. To do this, we have Romeo run around complimenting people with alliterations.

“I’m not sure I follow. How does writing out this play help you calculate Fizzbuzz?“, the interviewer asks.

Well you see, at any given time, there can only be two people on stage. Whoever is on the stage with Romeo will be affected by Romeo’s compliments.

When Romeo compliments an actor, each of Romeo’s nouns will count for “1”, and each adjective counts as a multiplier of 2, forming powers of 2.

So when Romeo tells Prince Henry through that he’s as rich as the “sum of a handsome happy honest horse and a lovely fellow”, the first part evaluates to 8 (3 adjectives, 1 noun = 2^3) and the second part just evaluates to 2 (1 adjective, 1 noun). This sets Prince Henry to 10.

Then, we say that Prince Henry is the “square of thyself”, where “thyself” is a reflexive noun referring to Prince Henry himself. This means Prince Henry will square his own value, setting him to 10^2 = 100.

We can then use Prince Henry as a comparator to check when our FizzBuzz program reaches 100.

We do the same with Ophelia to set her to 5, but only because obtaining multiples of 5 is inconvenient when everything is in powers of 2, so she’s more of a supporting actor in this play.

Lastly, Mercutio is the counter that goes from 1 to 100, so by calling him a “plum”, he will be initialized to 1, since all nouns are equal to 1.

And now, for the climax of the drama!


		   Scene II: A Pox Upon Both Houses.
Mercutio:
  Is the remainder of the quotient between myself and the difference between Ophelia and a warm wind as good as nothing?

Romeo:
  If so, let us proceed to scene V.

		   Scene III: What's In A Name.
Mercutio:
  Is the remainder of the quotient between myself and Ophelia as good as nothing?

Romeo:
  If so, let us proceed to scene VI.

		   Scene IV: You Shall Find Me A Grave Man.
Romeo:
  Open your heart!

Mercutio:
  Let us proceed to scene VII.

Here, we do our checks for whether Mercutio is a multiple of 3, 5, or neither. If he’s a multiple of 3 or 5, we will move over to scenes V and onwards, but if neither of those conditions are true, Romeo will compel Mercutio to open his heart. “Open your heart” is a code keyword in the Shakespeare language for “print your stored numerical value”.

And now for the play’s resolution!


		   Scene V: I Do Not Bite My Thumb At You.
Mercutio:
  Thou art the sum of a warm lamp and Ophelia.
  You are the product of thyself and the product of Ophelia and a brave squirrel.
  Speak your mind!

  You are the sum of yourself and the sum of a rich father and a mother. Speak your mind!

  Thou art the sum of the sum of the square of a cute cunning squirrel and a plum and thyself. 
  Speak your mind! Speak your mind!

  Is the remainder of the quotient between myself and Ophelia as good as nothing?

Romeo:
  If not, let us proceed to scene VII.

		   Scene VI: Wherefore Art Thou Romeo.
Mercutio:
  Thou art the sum of a fair fine angel and a gentle lovely flower. 
  You are the sum of a fair daughter and the square of thyself! Speak your mind!

  You are as charming as the sum of yourself and the square of a beautiful lovely lamp.
  Thou art the sum of thyself and the sum of a rich purse and a plum. Speak your mind!

  Thou art the sum of thyself and Ophelia. Speak your mind! Speak your mind!

		   Scene VII: Good Night, Good Night, Parting Is Such Sweet Sorrow.
Romeo: 
  You are as noble as the sum of yourself and a Lord. 

Mercutio:
  You are the product of Ophelia and a warm wind. Speak your mind!

Mercutio:
  Am I better than Prince Henry?

Romeo:
  If not, let us return to Scene II.
[Exeunt]

In order for us to print an ASCII character, we need one of the actors to set their value to the ASCII code for that character. Then, we trigger the printing of that ASCII character by having an actor say “Speak your mind!”.

In scenes V and VI, Mercutio and Romeo are in the scene, and Mercutio is setting Romeo’s values to the ASCII codes “70”, “73”, “90”, “90” for “FIZZ”, and “66”, “85”, “90”, “90” for “BUZZ” in scenes V and VI respectively.

In Scene V, which is when “FIZZ” is printed, there’s a possibility that the number isn’t also a multiple of 5, in which case we skip the “BUZZ” case via the “If (not/so), let us proceed to scene X” statement. This forces all of the actors on stage to switch to a different scene, without exiting or entering any new actors (ie; it’s a GOTO statement).

Lastly, by the time we get to scene VII, we increment Mercutio by one (by adding him to a noun, which counts for 1). If Mercutio’s value isn’t greater (better) than Prince Henry’s (100), then we loop back to Scene II, where we go through the process all over again until Mercutio’s value is over 100.

And of course, we will need new lines/line feeds for each new iteration, so we set Romeo to the product of Ophelia (5) and a warm wind (2) in order to get him to print out a new line character (ASCII code #10).

Impressed by the brilliance of your own play, you finally add the finishing [Exeunt] to your Shakespeare program to tell all of the actors to get off the stage, and just in time too — since the whiteboard’s run out of space.

The interviewer looks at you with a bewildered expression, no doubt impressed by your incredible Shakespearean prowess.

“So, did I get the job?”

Author’s note: If you want the source code, you can find it available here.

How To Get Your Company Hacked In Record Time

Henry Dang Java, security, Software Development ,

DISCLAIMER: This article is satire, and should not be taken seriously. Although the methods listed here will indeed get your company hacked in record time, this article was written to highlight security vulnerabilities that programmers should avoid. The methods used in this article are strictly for educational purposes, and should not be used for malicious reasons.

These days, it can be a struggle to get your company hacked. Between all of the new security patches that programmers push out on a day-to-day basis, and all of the fancy tools that you can use to statically analyze your code, getting hacked can be a chore.

Fortunately, I’ve learned some highly-effective methods that will get your company hacked in record time — even if it’s a multi-billion dollar company with tens of thousands of employees.

Method #1 – Publicly Leak Your Secrets Into Your Code

I know what you’re thinking. This is too obvious, isn’t it? It’ll get caught in code review, or by code analyzers. Fortunately for you, this method is really effective. How effective, you ask?

It’s so effective, that it caused a massive data privacy breach for over 57 million users for a certain multi-billion dollar company. Don’t worry if you’re not a multi-billion dollar company, because it works even for small companies and small projects, as evidenced by the over 100,000 leaked secrets on GitHub.

Here’s how to do it.

STEP 1 – Add this snippet anywhere in your company’s code. Remember to purposely ignore any password, secret, or key-vault/secret manager that your company might have.


    private String secretKey = "COMPANY_SECRET_KEY_HERE";

STEP 2 – Upload this code to your company’s preferred git repository.

Here, the path diverges based on how your company handles code reviews. If your company does a code review and notices the secret, then they will ask you to change your code. Fortunately, there is still a way to leak your company’s secret keys, even if they ask you to change your code.

The trick is to push the code with the secret, remove it, then push again. If your company approves the PR without squashing, then the leaked secret can be obtained by checking out the commit where you had added the secret, but before you had removed it.

As seen in the image above, by squashing, the commit with the leaked secret disappears and all of it turns into one commit. But if there’s no squashing, and the full history is retained, then you can access the commit history to checkout the commit with the leaked secret.

Method #2 – “Hide” Company Secrets In Slightly Less Plain Sight

This one is almost identical to method #1. The difference is that instead of blatantly being in plain sight, you’ve put a flimsy barrier in-between. For example, you can publish a client library with your secrets inside. Since it’s a client library, users seemingly shouldn’t be able to view the source code to extract your secrets.

Let’s illustrate the scenario. You are a consumer for this client library, and you see the following class structure for one of the client classes:


public class ClassWithSecret {
    private String secret;
    .... (other fields and methods)
}

Sadly, since this is a client library, programmers can’t modify the source code. And since it’s a private field, other programmers won’t be able to read it. Looks fool-proof, doesn’t it? With no way to access the source code, we can have the users use our clients without providing any configuration.

Luckily for us, it’s actually easy to completely side-step this issue, even if the field is private. All you have to remember is that “private” fields are not actually private. They’re a formality for saying, “don’t try to access me, and if you try to do it the normal way, it’ll fail”.

To access private fields, you just have to use reflection, which is a form of meta-programming that will let you modify the runtime behavior of a program. 


public class ClassWithSecret {
    private String secret;
}

// Assume we have a ClassWithSecret instance
ClassWithSecret classWithSecret = ....; 

try { 
    Field field = classWithSecret.getClass().getDeclaredField("secret");
    field.setAccessible(true);
    Object secretVal = field.get(classWithSecret);
    System.out.println("The secret was " + secretVal.toString());
} catch (Exception ex) {
    ...
}

By using reflection, we can just manually make the field accessible, and it will be as if it never had a private modifier.

The same thing applies to constants, readonly fields, and more. With reflection, you can override basically any behavior, so you can’t rely solely on language features to protect secrets or to guarantee specific behavior when it comes to client libraries.

In a different vein, another way that programmers often “hide” their secrets is through environmental variables, and one of the worst ways to do it is by putting your secrets into your .bashrc file. Although some may disagree, using environmental variables as a way to hold your secrets is generally bad practice.

However, putting your environmental variables into your .bashrc is absolutely catastrophically bad practice. The worst part is that the majority of online tutorials will actually tell you to do this (there’s a reason why people use key vaults and secret managers!)

So why does this make you susceptible to getting hacked? Because by putting your environmental variables into your .bashrc, you are injecting your environmental variables into every single process that runs on your user. If even a single one of these processes, or one of their child processes dies, they will almost certainly dump or log their environmental variables in some way, and once this happens, your secrets are now visible in your logs/log files. Boom. Your secrets are now in plain-sight.

For a more detailed explanation, check out what Diogo Monica, former security lead of Docker, has to say about this.

Method #3 – Forget About Getting Hacked Online, Get Hacked In-Person

Having your data leaked by online hackers is one thing, but what about getting hacked in-person?

It might sound strange, after all, when was the last time someone got hacked in-person? But getting hacked in-person is actually quite easy. All you have to do is scribble down your company’s passwords onto a piece of paper, or maybe a Post-it note.

Remember that the oldest surviving piece of paper, the Missal of Silos, still exists even after a thousand years, while the oldest known electronic computer, the Eniac Computer, has only existed for a measly 75 years. Therefore, a piece of paper is more durable than a computer, which is why you should be storing your passwords on Post-it notes, rather than something like LastPass.

Now that your password is in the physical realm, where it can safely survive for another thousand years under the right conditions, all you have to do is record a video of yourself with your password in the background. If a video is too difficult, you can alternatively take a photo instead.

Once your password has been leaked to the internet, your company will have successfully been hacked.

Conclusion

Getting hacked can be hard, but as long as you follow this guide, it’s as easy as 1-2-3. Just remember that there are more ways to get hacked than the ones listed above.

If you’re finding that getting hacked is just too easy, you can up the difficulty by using key vaults/secret managers, squashing commits in pull requests, and using static-code analyzers to check for leaked secrets. And most important of all, check your logs for secrets. Secrets should never show up in your logs, because logs are generally publicly visible (ie; in a dashboard or error tracking service).

Now that you know how to get hacked in record time, I challenge you to flip this article on its head, and see how long you can go without getting hacked. Good luck!

Learn OpenAPI in 15 Minutes

Henry Dang General Programming , ,

An OpenAPI specification (OAS) is essentially a JSON file that contains information about your RESTful API. This can be incredibly useful for documenting and testing your APIs. Once you create your OAS, you can use Swagger UI to turn your OAS into a living and interactive piece of documentation that other programmers can use.

Typically, there are libraries that can analyze all of your routes and automtaically generate an OAS for you, or at least a majority of it for you. Sometimes, it’s not feasible to generate it automatically, or you might want to understand why your OAS is not generating the correct interface.

So in this tutorial, we’ll learn OpenAPI in 15 minutes, starting right now.

First, here is the Swagger UI generated by the OAS we will be examining.

This is what an example “products” GET route with query parameters will look in Swagger UI when expanded:

And lastly, here is what a parameterized route will look like:

The routes can be tested inside of Swagger UI, and you can see that they are documented and simple to use. A Swagger UI page can easily be automatically generated if you have the OpenAPI spec (OAS) completed, so the OAS is really the most important part. Below are all of the major pieces of an OAS.


{
  # Set your OpenAPI version, which has to be at least 3.0.0
  "openapi": "3.0.0",
  # Set meta-info for OAS
  "info": {
    "version": "1.0.0",
    "title": "Henry's Product Store",
    "license": {
      "name": "MIT"
    }
  },
  # Set the base URL for your API server
  "servers": [
    {
      # Paths will be appended to this URL
      "url": "http://henrysproductstore/v1"
    }
  ],
  # Add your API paths, which extend from your base path
  "paths": {
     # This path is http://henryproductstore/v1/products"
    "/products": {
      # Specify one of get, post, or put
      "get": {
        # Add summary for documentation of this path 
        "summary": "Get all products",
        # operationId is used for code generators to attach a method name to a route
        # So operation IDs are optional, and can be used to generate client code
        "operationId": "listProducts",
        # Tags are for categorizing routes together
        "tags": [
          "products"
        ],
        # This is how you specify query parameters for your route
        "parameters": [
          {
            "name": "count",
            "in": "query",
            "description": "Number of products you want to return",
            "required": false,
            # Schemas are like data types
            # You can define custom schemas, which we will see later
            "schema": {
              "type": "integer",
              "format": "int32"
            }
          }
        ],
        # Document all possible responses to your routes
        "responses": {
          "200": {
            "description": "An array of products",
            "content": {
              "application/json": {
                "schema": {
                  # This "Products" schema is a custom type 
                  # We will look at the schema definitions near the bottom
                  "$ref": "#/components/schemas/Products"
                }
              }
            }
          }
        }
      },
      # This is a POST route on /products
      # If a route has two or more of a POST/PUT/GET, specify it as one route
      # with multiple HTTP methods, rather than as multiple discrete routes
      "post": {
        "summary": "Create a product",
        "operationId": "createProduct",
        "tags": [
          "products"
        ],
        "responses": {
          "201": {
            "description": "Product created successfully"
          }
        }
      }
    },
    # This is how you create a parameterized route
    "/products/{productId}": {
      "get": {
        "summary": "Info for a specific product",
        "operationId": "getProductById",
        "tags": [
          "products"
        ],
         # Parameterized route section is added here
        "parameters": [
          {
            "name": "productId",
            # For query parameters, this is set to "query" 
            # But for parameterized routes, this is set to "path"
            "in": "path",
            "required": true,
            "description": "The id of the product to retrieve",
            "schema": {
              "type": "string"
            }
          }
        ],
        "responses": {
          "200": {
            "description": "Successfully added product",
            "content": {
              "application/json": {
                "schema": {
                  # Custom schema called "Product"
                  # We will next examine schema definitions
                  "$ref": "#/components/schemas/Product"
                }
              }
            }
          }
        }
      }
    }
  },
  # Custom schema definitions are added here
  # Note that ints, floats, strings, and booleans are built-in
  # so you don't need to add custom schemas for those
  "components": {
    "schemas": {
      # define your schema name
      # custom schemas are referenced by "#/components/schemas/SCHEMA_NAME_HERE"
      "Product": {
        "type": "object",
        # define which of the properties below are required
        "required": [
          "id",
          "name"
        ],
        # define all of your custom schema's properties
        "properties": {
          "id": {
            "type": "integer",
            "format": "int64"
          },
          "name": {
            "type": "string"
          }
        }
      },
      # Sometimes you will want to return an array of a custom schema
      # In this case, this will return an array of Product items
      "Products": {
        "type": "array",
        "items": {
          "$ref": "#/components/schemas/Product"
        }
      }
    }
  }
}

If you want to try out the OAS above, here is a version of it with no comments that can be passed into Swagger UI or any Swagger editor, like https://editor.swagger.io/.


{
  "openapi": "3.0.0",
  "info": {
    "version": "1.0.0",
    "title": "Henry's Product Store",
    "license": {
      "name": "MIT"
    }
  },
  "servers": [
    {
      "url": "http://henrysproductstore/v1"
    }
  ],
  "paths": {
    "/products": {
      "get": {
        "summary": "Get all products",
        "operationId": "listProducts",
        "tags": [
          "products"
        ],
        "parameters": [
          {
            "name": "count",
            "in": "query",
            "description": "Number of products you want to return",
            "required": false,
            "schema": {
              "type": "integer",
              "format": "int32"
            }
          }
        ],
        "responses": {
          "200": {
            "description": "An array of products",
            "content": {
              "application/json": {
                "schema": {
                  "$ref": "#/components/schemas/Products"
                }
              }
            }
          }
        }
      },
      "post": {
        "summary": "Create a product",
        "operationId": "createProduct",
        "tags": [
          "products"
        ],
        "responses": {
          "201": {
            "description": "Product created successfully"
          }
        }
      }
    },
    "/products/{productId}": {
      "get": {
        "summary": "Info for a specific product",
        "operationId": "getProductById",
        "tags": [
          "products"
        ],
        "parameters": [
          {
            "name": "productId",
            "in": "path",
            "required": true,
            "description": "The id of the product to retrieve",
            "schema": {
              "type": "string"
            }
          }
        ],
        "responses": {
          "200": {
            "description": "Successfully added product",
            "content": {
              "application/json": {
                "schema": {
                  "$ref": "#/components/schemas/Product"
                }
              }
            }
          }
        }
      }
    }
  },
  "components": {
    "schemas": {
      "Product": {
        "type": "object",
        "required": [
          "id",
          "name"
        ],
        "properties": {
          "id": {
            "type": "integer",
            "format": "int64"
          },
          "name": {
            "type": "string"
          }
        }
      },
      "Products": {
        "type": "array",
        "items": {
          "$ref": "#/components/schemas/Product"
        }
      }
    }
  }
}

The Curious npm Package With Over 60M Downloads

Henry Dang javascript, npm, Software Development , , , , , ,

The node package manager, also known as npm, is a crucial part of the Javascript library ecosystem. Many of the most popular JS libraries and frameworks, such as ReactJS, JQuery, AngularJS, etc., are primarily downloaded from npm.

In fact, there’s one curious little npm package with over 60 million downloads, a package so incredibly useful and revolutionary that nearly every JS developer has installed this, or one of its dependents at least once in their lives. Have you ever used WebPack or ReactJS? Because both of those packages are dependents of this aforementioned mysterious package.

And the name of that revolutionary package? It’s is-odd. A package whose only purpose is to tell you whether a number is odd or not.

So What Else Does Is-Odd Do?

You’re probably thinking that there’s no way a package whose only job is to tell you if a number is odd or not, could possibly accrue 60 million downloads. Surely, it must do something else.

Fortunately, the source code never lies. 

const isNumber = require('is-number');

module.exports = function isOdd(value) {
  const n = Math.abs(value);
  if (!isNumber(n)) {
    throw new TypeError('expected a number');
  }
  if (!Number.isInteger(n)) {
    throw new Error('expected an integer');
  }
  if (!Number.isSafeInteger(n)) {
    throw new Error('value exceeds maximum safe integer');
  }
  return (n % 2) === 1;
};

Aside from doing type checking to ensure that something is actually a number, it quite literally only runs (n % 2 == 1)

And that’s it. Over 60 million downloads, to run a single line of code.

“But what about all of the type checking?”. The type checking is a non-issue, because if it was ever a problem, then that means your code has an edge case that makes nearly no sense. For example, how would it ever be possible for you to accidentally check if a string is an even number, and not have this mistake get caught somewhere else in your code, like the input/data-fetching step?

Furthermore, if you seriously anticipate that the type might be wrong, then you would also have to wrap your code in a try catch statement. If you’re still not convinced, we can attempt to extend this philosophy by deprecating the “+” operator in JavaScript and replacing it with this function:

const isNumber = require('is-number');

module.exports = function add-numbers(value1, value2) {
  if (!isNumber(value1)) {
    throw new TypeError('expected a number for first input');
  }
  if (!isNumber(value2)) {
    throw new TypeError('expected a number for second input');
  }
  return value1 + value2
};

Now, anytime you want to add two numbers, you can’t just do value1 + value2. You’d have to do this instead:

try {
  add-numbers(value1, value2)
} catch(err) {
  console.log("Error! " + err);
}

But there’s a glaring problem here. With the is-odd package, we can check if a number is odd, but what if it’s even? Which of these three things would you do?

  1. Simply write (n % 2 == 0)
  2. The opposite of odd is even, so just do !isOdd(n)
  3. Create an entirely new npm package, complete with a test suite, TravisCL integration, and an MIT License.

Both 1 and 2 are the obvious sensible options, and yet, option 3, which is the aptly-named is-even package, was the option of choice.

So we’ve created an entirely new npm package, which has its own set of dependents. And this package has over 100,000 weekly downloads! What’s in the source code, then?

var isOdd = require('is-odd');

module.exports = function isEven(i) {
  return !isOdd(i);
};

A one-liner, with no logic other than reversing the result of another package’s function. And it’s dependency is is-odd!

So what exactly is wrong with having all of these tiny and largely useless dependencies? The more dependencies your project has, especially if those dependencies are not from verified and secure sources, the more likely you are to face security risks.

Like that one time a popular npm package spammed everyone’s build logs with advertisements, causing npm to ban terminal ads, or perhaps that other scandal where a core npm library tried to steal people’s cryptocurrencies.

Dependencies should be useful, non-trivial, and secure, which is why packages like is-even and is-odd don’t make any sense from a developmental standpoint. They’re so incredibly trivial (one-liners), that even adding them to your project is just a massive security and developmental risk with zero upside. Unfortunately, is-odd is firmly cemented in the history of npm, and most major packages include it as an essential dependency. There is no escape from single-line npm packages anytime in the foreseeable future.

How To Reduce Vision and Image Processing Times

Henry Dang General Programming, machine learning, Software Development , , ,

Have you ever tried writing a program to analyze or process images? If so, you’re likely no stranger to the fact that analyzing large numbers of images can take forever. Whether you’re trying to perform real-time vision processing, machine learning with images, or an IoT image processing solution, you’ll often need to find ways to reduce the processing times if you’re handling large data sets.

All of the techniques listed in this article take advantage of the fact that images more often than not have more data than needed. For example, suppose you get a data set full of 4K resolution full-color images of planes. We’ll use this image below to track our optimization steps.

Removing Colors

There are many situations in which color is necessary. For example, if you’re trying to detect fresh bloodstains in an image, you normally wouldn’t turn an image into grayscale. This is because all fresh bloodstains are red, and so you would be throwing away critical information if you were to remove the color from an image.

However, if color is not necessary, it should be the first thing that you remove from an image to decrease processing times.

The reason removing color from an image decreases processing time is because there are fewer features to process, where we’ll say a feature is some measurable property.

With RGB (red, green, blue, ie; colored images), you have three separate features to measure, whereas with grayscale, you only have one. Our current plane image should now look like this:

Using Convolution Matrices

A convolution matrix, also known as a mask or a kernel, is a 3×3 or 5×5 matrix that is applied over an entire image. For this article, we will examine only 3×3 matrices.

For a 3×3 matrix, we select a 3×3 square in the image, and for each pixel, we multiply that pixel by its corresponding matrix position. We then set the pixel in the center of that 3×3 square to the average of those 9 pixels after the multiplication.

If you wanted this to output visually, you can simply set a pixel to 0 if it’s less than 0, and 255 if it’s greater than 255.

Immediately, you might realize that if we have to select a 3×3 square in the original image, then our convolution matrix would be useless if we selected the top left pixel. If the top left pixel is selected, then you wouldn’t be able to create a 3×3, since you would only have 4 pixels from the 3×3 (ie; you’d have a 2×2) and would be missing the remaining 5 pixels.

There are a wide variety of ways to handle these cases, although we won’t cover them in any depth in this article. For example, You could duplicate the 2×2 four times, by rotating the 2×2 around the center pixel to fill in the missing pixels, or you could just trivially set the missing pixels to 0 (results may be poor if you do this though).

There are massive lists of convolution matrices that can do all sorts of things from sharpening, blurring, detecting vertical lines, and detecting horizontal lines. Here’s our plane after applying a convolution matrix for detecting horizontal lines. Specifically, this matrix is [(-1, -1, -1), (2, 2, 2), (-1, -1, -1)]

Similarly, here’s the result after applying a convolution matrix for detecting vertical lines. The matrix for this one is [(-1, 2, -1), (-1, 2, -1), (-1, 2, -1)].

You might be wondering, “But how does this help me? It doesn’t reduce processing times at all!”. And you’re right. This only makes your processing time longer. However, notice that once you use convolution to extract out the high-level details you want, like edges, your image now has a lot of the excessive noise removed. For example, in the image above, you can see that the sky is no longer in the image.

This means that we’ve isolated the important parts of the images, which allows us to safely reduce the size of the resulting matrix without a huge loss in detail.

SIDE NOTE: You may be wondering why we can’t just downsize the image before we perform any processing steps on it. The reason for this is that if you downsize the image right away, you will almost always lose important detail. Additionally, downsizing an image can create artifacts, and if you are looking for particularly small details, like a 2-4 pixel pattern in a large image, you will almost certainly lose that detail when you scale down the image. This is why you should capture those details first before scaling down.

Pooling

In a nutshell, pooling is a technique to reduce the size of a matrix. You pool after you apply your convolutions, because each time you pool, you will lose some features.

Generally, each cycle of pooling will decrease the number of features in your image by some multiplicative constant. It’s trivial to see that if you continuously pool your image over and over again, you will eventually lose too much detail (like if you pooled until you just had a single 1×1 matrix).

Pooling works by first selecting an arbitrarily sized square. Let’s say you want to use a 4×4 square. The goal of pooling is to take this 4×4 square in a matrix, and reduce it to a single 1×1 matrix. This can be done in many ways. For example, max pooling is when you take the maximum value in that 4×4 matrix, average pooling is when you average all the values of the matrix, and min pooling is when you take the minimum value from the matrix.

As a rule of thumb, you will want to use max pooling since that captures the most prominent part of the 4×4 matrix. For example, in edge detection, you would want to use max pooling because it would downsize the matrix while still showing you the location of the edges.

What you would not use is min pooling, because if there is even a single cell where no edge was detected inside a 4×4 matrix that is otherwise full of edges, the pooling step would leave you with a value of 0, indicating that there was no edge in that 4×4 matrix.

For a better understanding of why you should pool, consider the fact that a 4K image is a 3840 x 2160 image, which is 8,294,400 individual features to process. Suppose we can process ten 4K images a second (82,940,000 features a second). Let’s compare the original 3840 x 2160 representation versus a 480 x 270 pooled representation.

# Images3840 x 2160 image (time)480 x 270 image (time)
101 second0.015625 seconds
1,00016.67 minutes1.56 seconds
1,000,00011.57 days26.04 minutes
1,000,000,00031.71 years18.0844 days

At ten 4K images a second, it would take over 30 years to process a million images, whereas it would only take 18 days if you had done pooling.

Conclusion

When processing images, especially high-resolution images, it’s important that you shrink down the number of features. This can be done through many methods. In this article, we covered converting an image to grayscale, as well as techniques such as convolution to extract important features, and then pooling to reduce the spatial complexity.

In this article, we compared the difference between pooling and not pooling, and found that the difference of analyzing a million 4K grayscale image without pooling would take 31 years, versus 18 days if we had pooled it down to a 480 x 270 image. However, not turning the images into grayscale can also have a noticeable effect.

As a final food for thought, if you had performed none of the optimizations mentioned in this article, analyzing a million full-color 4K resolution images with convolutions would take nearly an entire century, versus a measly 18 days if you had turned them into grayscale and then performed convolution and pooling.

In other words, with no optimizations, your image processing would take so long, that you could be rolling in your grave, and your program still wouldn’t be done running.